1.最早的人工神经元的数学模型，没有权重

2.感知器增加了权重

3.感知器怎么样能训练出权重?

买房子的例子，有很多影响因素，譬如房价、面积、位置、楼层，这些因素的影响权重是不同的，那训练出权重，感知器就能预测，对于给定的一套房子，人们对这套房子的购买意向有多大。

首先，所有的权重参数都是随机的；然后根据一个标准【代价函数】，使用一些方法【梯度下降】更新权重，直到这个标准【代价函数】的值足够好；或者权重每次更新的值足够小。

3.1什么是代价函数？

​ 在我们这里的例子中，感知器的代价函数是预测值（找出的那条最优线）和训练值差（已知的数据，统计到的数据）的平方和(所有的点到预测那条线的垂直距离之和最小，均方差最小，要达到这样一个标准，最小化这个标准，那这个标准我们称之为代价函数，或者是损失/lost函数,加粗的就是代价函数，常见的代价函数就是下面的最小均方)

3.2什么是梯度下降？

​ 梯度下降就是沿着代价函数的梯度减小代价函数的过程。梯度下降是一个非常重要的概念，

梯度下降中的梯度指的是代价函数对各个参数的偏导数，偏导数的方向决定了在学习过程中参数下降的方向，学习率（通常用α表示）决定了每步变化的步长，有了导数和学习率就可以使用梯度下降算法（Gradient Descent Algorithm）更新参数了。

现在给定的目标是房价 或者 ，x是输入房子的面积，w是权重，b是偏差；我们希望找出来w和b，尽可能接近真实情况。

3.2.1什么是 损失函数（就是代价函数）？什么是最小均方？

预测出来的值 - 真实的值 求个平方和， 再求个平均。

• 损失函数是w和b的函数

给定损失函数是最经常使用的就是最小均方(xi yi 是已知的，是点)，

如果w和b能让最小均方【损失函数】达到最小，那么就是最优的w和b。

为什么一个是/2m , 一个是/m 。 定义是/m.求导方便是/2m

(怎样计算w和b?,有闭形式和没有闭形式的，后者用梯度下降)

(均方差)标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。)

x,y轴就是w,b z轴是lost(w,b),最小化损失函数，就是在这个三维的图中找到最小的值，怎么快速准确的找到最小的点？

沿切线的方向走，最快，就是求导，分别对w和b求导,方向找到了，那要走多远，那就是学习率的问题，学习率呢，就是超参数，需要调参数。

3.2.2什么是学习率，什么叫学习？参数是怎么更新的

梯度下降是为了最小化损失函数。最小化损失函数是为了找到合适的系数w(权重)和b(偏差)。

标准梯度下降，每次更新要把所有训练数据都考虑到。

要进行逐步优化，必须有（2？）个初始值。初始值是w,b随机选的。选出来这两个值之后，算一下。更多情况是，一算发现，不好，差挺远的，那赶紧改进一下。

怎么改进？

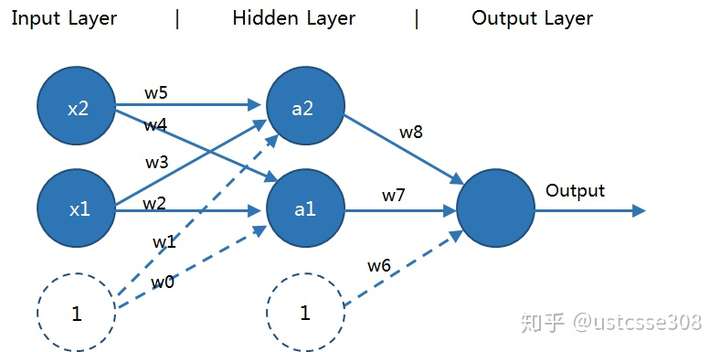
问题：

在以上的网络中，每一层的参数的维度是多少？

输入层到隐藏层 的w的维度 是 2 * 3的

本次课内容

• 历史和一些概念

• 第一段代码

• 第二段代码

• sigmoid函数与交叉熵