损失函数

梯度下降

这里没弄懂，后面会有问题的。

什么样的算法能够模拟人来做出决定呢？机器学习的算法。

神经网络在近几年的快速发展，算法在一些任务上已经超过了人类。那么到底什么是神经网络？

人类在漫长的进化过程中，大脑细胞形成了一套有效的工作机制。

科学家发现大脑细胞是怎么样工作的？

• 1943年，某科学家用一个简单的数学模型表达了神经元信号传递的方式——整合多个信号输入并转化为一个信号输出给其他神经元。 什么是阶跃函数？

这个模型的问题？

不同的输入需要区别对待。

• 受这个对于人脑学习方式的认知的启发，1956年弗兰克·罗森布拉特进一步改善了人工神经元设计，增加了类似于人脑的学习机制，这个模型叫做感知器（Perceptron）。 增加权重是一个非常重要的改进。

一些重要概念

• 输入向量Input

• 阶跃函数

• 权重

• 感知器 感知器是对神经元的直接模拟。

感知器的工作过程实际上就是首先训练，然后预测。 那么感知器怎么样能训练出权重呢？

梯度下降是什么(就是求函数最小值)

1.

为什么梯度下降算法（BGD批量梯度下降）用的是所有样本点梯度的均值作为最终的梯度方向？

https://www.zhihu.com/question/66368329/answer/261909009

2.

https://www.bilibili.com/video/BV1B741187Kh?from=search&seid=6240937086872409352

梯度下降法原理与代码实战案例

【01：03：00】随机梯度下降

通过一个简单的例子，来理解一下权重的训练过程。

这条线就是x前面的系数 y前面的系数 + b。 这条线把4个点分成了2类 。

XOR就是感知机无法处理非线性情况的证明。

使用一层的感知机可以准确地描述AND和OR，使用两层的感知机就可以描述异或。

虽然感知器的结构很简单，但是感知器可以用来解决很多的线性可分的问题；但是一旦遇到非线性可分的问题时，它就不管用了。

【01：44：00】开始介绍神经网络

正如在数学上，XOR可以通过使用AND和OR的组合来实现一样，单层感知机不能解决的问题，通过多个单层连接在一起就可以解决了。

• 我们把连接在一起的多层的系统称作神经网络，单个感知机称为是神经元；
• 神经元和感知器本质上是一样的，只不过我们说感知器的时候，它的激活函数是阶跃函数；
• 而当我们说神经元时，激活函数往往选择为sigmoid函数或tanh函数，同时，在使用了sigmoid函数之后，一般使用交叉熵作为损失函数。

神经网络的定义

• 神经元按照层来布局。最左边的层叫做输入层，负责接收输入数据；最右边的层叫输出层，我们可以从这层获取神经网络输出数据。输入层和输出层之间的层叫做隐藏层，因为它们对于外部来说是不可见的。
• 同一层的神经元之间没有连接。第N-1层神经元的输出就是第N层神经元的输入，如果第N层的每个神经元和第N-1层的所有神经元相连(就是full connected)，。
• 每个连接都有一个权值。

反向传播

Sigmod函数

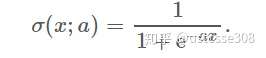
a用于控制sigmoid函数的形状，在神经网络中，a一般取1。

交叉熵函数定义

代码实现

关于激活函数（***要考）

深度学习的基本原理是基于人工神经网络，信号从一个神经元进入，经过非线性的激活函数，传入到下一层神经元；再经过该层神经元的激活，继续往下传递，如此循环往复，直到输出层。正是由于这些非线性函数的反复叠加，才使得神经网络有足够的能力来抓取复杂的特征。加入激活函数，是为了增强模型的非线性，如果不经过非线性激活，那么无论神经网络加多少层永远都是线性组合，而加入了非线性激活函数后，已经可以证明，可以以任意精度逼近非线性函数。显而易见，激活函数在深度学习中举足轻重。

激活函数最早起源于生物学，神经生物学认为一个神经元细胞要么处于激活状态，要么是抑制状态，人工神经网络目的之一就是要模拟这一机制，所以就按照这个机理设计了二值化激活过程，也就是说超过某一个阈值就取值1，代表激活，低于某个阈值就取值0，代表抑制。

画出这种特性的函数的图像，0-1二值化激活其实就是最著名的阶跃函数。这个0-1激活函数很符合仿生学的要求，但是数学性质不好。因为不连续所以不可导，在断点处导数无穷大，不利于后续的数学分析，而一般的反向传播神经网络都需要反向求导过程。

因此引入了sigmoid函数，这个函数在函数图像上很接近阶跃函数，范围是从0-1，而且具备了极好的数学性质，便于数学推导。Sigmoid函数是深度学习领域开始时使用频率最高的激活函数。

但是sigmoid自己也存在问题，sigmoid函数的微分的最大值是当取值为0的时候，也就是1/4；当反向传播经过多层之后，梯度会变得非常小，导致参数更新很慢。

几个常见的激活函数：

1.sigmoid函数：

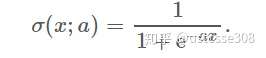
其中，a用于控制sigmoid函数的形状，在神经网络中，a一般取1。

Sigmoid函数的导数：

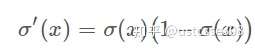
Sigmoid 函数和导数画图如下 ：

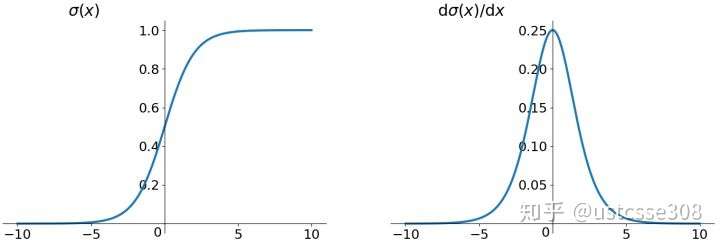
特点：它能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.

2.Tanh函数全称Hyperbolic Tangent，即双曲正切函数，定义如下：

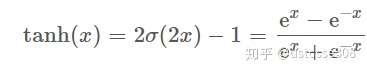
导数如下：

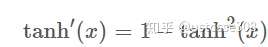
Tanh函数和导数：

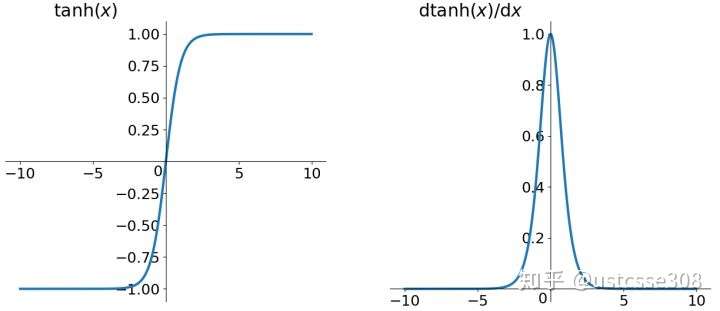
3.Sigmoid 和 tanh 两个函数非常相似，具有不少相同的性质。简单罗列如下

• 优点：平滑
• 优点：易于求导
• 缺点：幂运算相对耗时
• 缺点：导数值小于 1，反向传播易导致梯度消失（Gradient Vanishing）

对于 Sigmoid 函数来说，它的值域是 (0,1)，因此又有如下特点

• 优点：可以作为概率，辅助模型解释
• 缺点：输出值不以零为中心，可能导致模型收敛速度慢

4.梯度消失

使用BP，也即导数的后向传递来优化：先计算输出层对应的损失，然后将损失以导数的形式不断向上一层网络传递，修正相应的参数，达到降低损失的目的。 Sigmoid函数在深度网络中常常会导致导数逐渐变为0，使得参数无法被更新，神经网络无法被优化。原因在于两点：(1) 在上图中容易看出，当)中较大或较小时，导数接近0，而后向传递的数学依据是微积分求导的链式法则，当前层的导数需要之前各层导数的乘积，几个小数的相乘，结果会很接近0 (2) Sigmoid导数的最大值是0.25，这意味着导数在每一层至少会被压缩为原来的1/4，通过两层后被变为1/16。不同的层次计算出来的梯度的大小不同，越靠前的层的学习速度就越慢。也就是，梯度消失的问题。

5.ReLU函数(Rectified Linear Units)其实就是一个取最大值函数。

虽然它形式非常简单，但是它比较好地解决了梯度消失的问题，而且计算速度非常快，只需要判断输入是否大于0，收敛速度远快于sigmoid和tanh。它是比较常用的激活函数。