首先看一下基于词典的方法；然后基于统计的方法，我们讨论一下HMM。

正向最大匹配思想MM

1. 从左向右取待切分汉语句的m个字符作为匹配字段，m为大机器词典中最长词条个数。

\2. 查找大机器词典并进行匹配。若匹配成功，则将这个匹配字段作为一个词切分出来。

若匹配不成功，则将这个匹配字段的最后一个字去掉，剩下的字符串作为新的匹配字段，进行再次匹配，重复以上过程，直到切分出所有词为止。

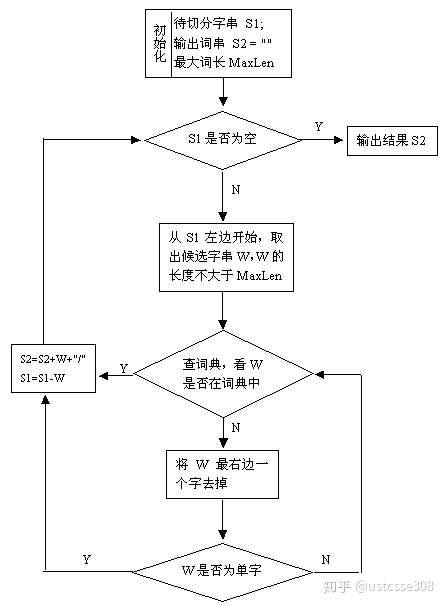
逆向最大匹配算法RMM

该算法是正向最大匹配的逆向思维，匹配不成功，将匹配字段的最前一个字去掉，实验表明，逆向最大匹配算法要优于正向最大匹配算法。

双向最大匹配法(Bi-directction Matching method,BM)

双向最大匹配法是将正向最大匹配法得到的分词结果和逆向最大匹配法的到的结果进行比较，从而决定正确的分词方法。据SunM.S. 和 Benjamin K.T.（1995）的研究表明，中文中90.0％左右的句子，正向最大匹配法和逆向最大匹配法完全重合且正确，只有大概9.0％的句子两种切分方法得到的结果不一样，但其中必有一个是正确的（歧义检测成功），只有不到1.0％的句子，或者正向最大匹配法和逆向最大匹配法的切分虽重合却是错的，或者正向最大匹配法和逆向最大匹配法切分不同但两个都不对（歧义检测失败）。这正是双向最大匹配法在实用中文信息处理系统中得以广泛使用的原因所在。

这个思想很简单，相对应的代码，也比较简单。以下代码参考：

https://github.com/senpai-a/chinese-word-segmentationgithub.com

# -*- coding:utf8 -*-
import codecs
import string
import re
import sys

def load_dict(filename):  
    f = open(filename,'r',encoding="utf-8").read()  
    maxLen = 1  
    dict=f.split("\n")
    for i in dict:  
        if len(i)>maxLen:  
            maxLen=len(i)  
  
    return dict,maxLen;  
  
#分词 返回分好的列表
def maxlen_segmentation(dict,maxLen,sentence,foreward=True):
	wordList=[]  #结果
	i=0
	j=0
	while(len(sentence)>0):
		n = len(sentence)
		if foreward:
			word=sentence[0:maxLen]
		else:
			word=sentence[n-maxLen:n]

		found=False;   #是否找到词  
  
		while((not found) and (len(word)>0)):
			if(word in dict):  #命中
				wordList.append(word+'  ')
				print("命中 %s"%word)
				i+=len(word)
				if foreward:
					sentence=sentence[len(word):n]#后移
				else:
					sentence=sentence[0:n-len(word)]#前移
					#print("下一个 %s"%sentence)
					#input();
				found=True;
			else:  
                #当词长为1时,强行命中  
				if(len(word)==1):  
					wordList.append(word+'\n')
					#print("单字 %s"%word)
					i+=len(word)					
					if foreward:
						sentence=sentence[len(word):n]#后移
					else:
						sentence=sentence[0:n-len(word)]#前移
						#print("下一个 %s"%sentence)
						#input();
					found=True; 
				else:
					if foreward:
						word=word[0:len(word)-1]
					else:
						word=word[1:len(word)]
						#print(word)

	return wordList  
  
def main():
	"""if len(sys.argv)!=3:
		print('用法：seg.py 词典文件名 输入文件名')
		return
	"""
	#dict,maxLen=load_dict(sys.argv[1])
	dict,maxLen=load_dict("dict.txt")
	#strIn = open(sys.argv[2],encoding="utf-8").read()
	strIn = open("in.txt", encoding="utf-8").read()
	
	print("开始分词...\n")
	
	f_result=maxlen_segmentation(dict,maxLen,strIn,True)	
	b_result=maxlen_segmentation(dict,maxLen,strIn,False)
	print('前向最大匹配分词：%d个词'%len(f_result))
	print('后向最大匹配分词：%d个词'%len(b_result))
	
	open('foreward.txt','w',encoding="utf-8").writelines(f_result)
	open('backward.txt','w',encoding="utf-8").writelines(b_result[::-1])
	print('结果已保存在foreward.txt backward.txt')
  
if __name__ == '__main__':  
	main()

看一下运行效果。

前向效果：

我  是  中国  人  

腾  讯  和  阿里  都  在  新  零售  大举  布局  

结婚  的  和尚  未  结婚  的  

南京市  长江  大桥  

我  在  学生  物

后向效果：

我  是  中  国人  

腾  讯  和  阿里  都  在  新  零售  大举  布局  

结婚  的  和  尚未  结婚  的  

南京市  长江  大桥  

我  在  学  生物

因为它是基于词典的，所以分词效果的好坏很大程度上取决于词典本身的精确程度。

---

接下来看一下基于统计的方法。

以下例子来自于参考12和，在此表示感谢。

这里首先介绍下n-gram。

N-gram的第一个特点是某个词的出现依赖于其他若干个词，第二个特点是我们获得的信息越多，预测越准确。正式来说，N-gram模型是一种语言模型（Language Model，LM），语言模型是一个基于概率的判别模型，它的输入是一句话（单词的顺序序列），输出是这句话的概率，即这些单词的联合概率（joint probability）。

N-gram本身也指一个由NNN个单词组成的集合，各单词具有先后顺序，且不要求单词之间互不相同。常用的有 Bi-gram (N=2N=2N=2) 和 Tri-gram (N=3N=3N=3)，一般已经够用了。例如在上面这句话里，我可以分解的 Bi-gram 和 Tri-gram ：

Bi-gram : {I, love}, {love, deep}, {love, deep}, {deep, learning}
Tri-gram : {I, love, deep}, {love, deep, learning}

假设一个字符串s由m个词组成，因此我们需要计算出P(w1,w2,⋯,wm)的概率，根据概率论中的链式法则得到如下：

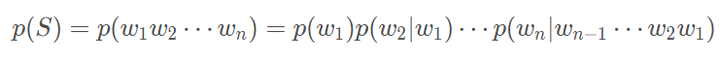
直接计算这个概率的难度有点大，因此引入马尔科夫假设（Markov Assumption）：一个词的出现仅与它之前的若干个词有关，即

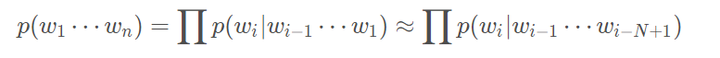
，其中i为某个词的位置，n为定义的相关的前几个词，因此得到如下：

当n=1时，即一元模型（Uni-gram）

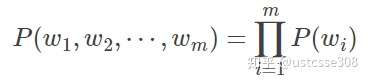
但 n=2时，即二元模型（Bi-gram）

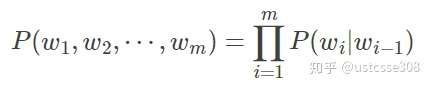
当n=3时，即三元模型（Tri-gram）

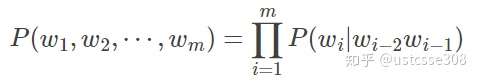
N可以取很高，然而现实中一般 bi-gram 和 tri-gram 就够用了；而且N取得太大，会导致参数空间过大和数据稀疏严重等问题，因为词同时出现的情况可能没有。

如何计算其中的每一项条件概率呢？答案是极大似然估计（Maximum Likelihood Estimation，MLE），简单点就是计算频率：

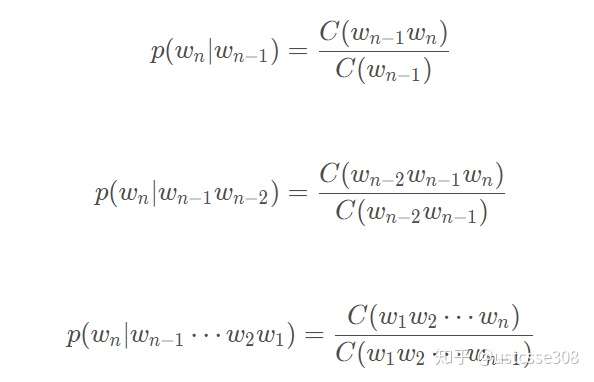
具体地，以Bi-gram为例，我们有这样一个由三句话组成的语料库：

容易统计，“I”出现了3次，“I am”出现了2次，因此能计算概率：

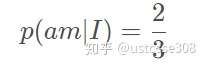
同理，还能计算出如下概率：

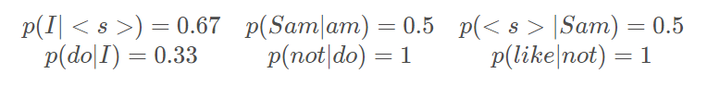
另外再提供一个《Language Modeling with Ngrams》中的例子，Jurafsky et al., 1994 从加州一个餐厅的数据库中做了一些统计：

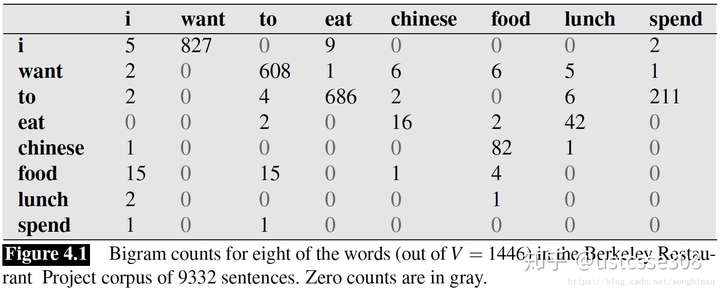
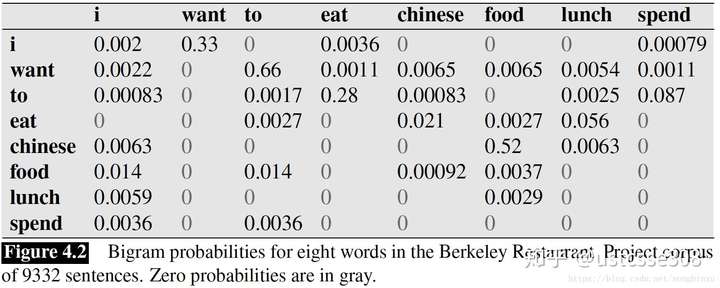
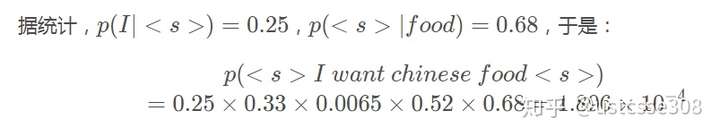
因此算出了“I want chinese food”这句话的概率，但有时候这句话会很长，那么概率（都是小于1的常数）的相乘很可能造成数据下溢（downflow），即很多个小于1的常数相乘会约等于0，此时可以使用log概率解决。

---

结合jieba分词来看一下。

以下内容来自参考8，在此表示感谢。

jieba分词主要是基于统计词典，构造一个前缀词典；然后利用前缀词典对输入句子进行切分，得到所有的切分可能，根据切分位置，构造一个有向无环图；通过动态规划算法，计算得到最大概率路径，也就得到了最终的切分形式。

实例讲解

以“去北京大学玩”为例，作为待分词的输入文本。

离线统计的词典形式如下，每一行有三列，第一列是词，第二列是词频，第三列是词性。这里需要强调一下，北 17860这一项，是’北’这个字，作为单独词素出现的，譬如像’向北走’，类似地，’京’也是像’赴京赶考’这样的情况。

...
    北京大学 2053 nt
    大学 20025 n
    去 123402 v
    玩 4207 v
    北京 34488 ns
    北 17860 ns
    京 6583 ns
    大 144099 a
    学 17482 n
    ...

前缀词典构建

首先是基于统计词典构造前缀词典，如统计词典中的词“北京大学”的前缀分别是“北”、“北京”、“北京大”；词“大学”的前缀是“大”。统计词典中所有的词形成的前缀词典如下所示，你也许会注意到“北京大”作为“北京大学”的前缀，但是它的词频却为0，这是为了便于后面有向无环图的构建。因为，在后面计算DAG的时候，’北京大’可以作为后面还可以可以到达的词的一个指示，可以结合后面的代码理解。

...
    北京大学 2053
    北京大 0
    大学 20025
    去 123402
    玩 4207
    北京 34488
    北 17860
    京 6583
    大 144099
    学 17482
    ...

看一下代码：

for line in f:
    try:
        line = line.strip().decode('utf-8')
        word, freq = line.split()[:2]
        freq = int(freq)
        self.wfreq[word] = freq
        for idx in range(len(word)):
            wfrag = word[:idx + 1]
            if wfrag not in self.wfreq:
                self.wfreq[wfrag] = 0  # trie: record char in word path
        self.total += freq
        count += 1

有向无环图构建

然后基于前缀词典，对输入文本进行切分，对于“去”，没有前缀，那么就只有一种划分方式；对于“北”，则有“北”、“北京”、“北京大学”三种划分方式；对于“京”，也只有一种划分方式；对于“大”，则有“大”、“大学”两种划分方式，依次类推，可以得到每个字开始的前缀词的划分方式。

在jieba分词中，对每个字都是通过在文本中的位置来标记的，因此可以构建一个以位置为key，相应划分的末尾位置构成的列表为value的映射，如下所示，

0: [0]
1: [1,2,4]
2: [2]
3: [3,4]
4: [4]
5: [5]

对于0: [0]，表示位置0对应的词，就是0 ~ 0，就是“去”；对于1: [1,2,4]，表示位置1开始，在1，2，4位置都是词，就是1 ~ 1，1 ~ 2，1 ~ 4，即“北”，“北京”，“北京大学”这三个词。

对于每一种划分，都将相应的首尾位置相连，例如，对于位置1,可以将它与位置1、位置2、位置4相连接，最终构成一个有向无环图，如下所示，

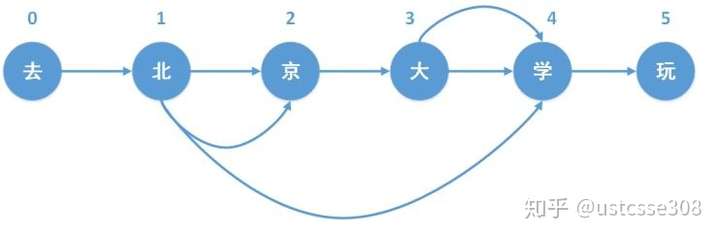
最大概率路径计算

在得到所有可能的切分方式构成的有向无环图后，我们发现从起点到终点存在多条路径，多条路径也就意味着存在多种分词结果，例如，

# 路径1
    0 -> 1 -> 2 -> 3 -> 4 -> 5
    # 分词结果1
    去 / 北 / 京 / 大 / 学 / 玩
    # 路径2
    0 -> 1 , 2 -> 3 -> 4 -> 5
    # 分词结果2
    去 / 北京  /  大 / 学 / 玩
    # 路径3
    0 -> 1 , 2 -> 3 , 4 -> 5
    # 分词结果3
    去 / 北京  /  大学  /  玩
    # 路径4
    0 -> 1 , 2 , 3 , 4 -> 5
    # 分词结果4
    去 / 北京大学    /     玩
    ...

因此，我们需要计算最大概率路径，也即按照这种方式切分后的分词结果的概率最大。在计算最大概率路径时，jieba分词采用从后往前这种方式进行计算。为什么采用从后往前这种方式计算呢？因为，我们这个有向无环图的方向是从前向后指向，对于一个节点，我们只知道这个节点会指向后面哪些节点，但是我们很难直接知道有哪些前面的节点会指向这个节点。

可以想一下对于“去 北 京 大 学 玩”，如果我们想要从前向后计算到达‘学’字的最大概率，那么必须要知道由前面哪几个字可以到达‘学’字。但是从‘学’字出发计算到‘玩’字的最大概率是可以计算得出的。

在采用动态规划计算最大概率路径时，每到达一个节点，它前面已经计算的节点到终点的最大路径概率已经计算出来。

有向无环图构建

有向无环图，directed acyclic graphs，简称DAG，是一种图的数据结构，顾名思义，就是没有环的有向图。

DAG在分词中的应用很广，无论是最大概率路径，还是其它做法，DAG都广泛存在于分词中。因为DAG本身也是有向图，所以用邻接矩阵来表示是可行的，但是jieba采用了Python的dict结构，可以更方便的表示DAG。最终的DAG是以{k : [k , j , ..] , m : [m , p , q] , …}的字典结构存储，其中k和m为词在文本sentence中的位置，k对应的列表存放的是文本中以k开始且词sentence[k: j + 1]在前缀词典中的 以k开始j结尾的词的列表，即列表存放的是sentence中以k开始的可能的词语的结束位置，这样通过查找前缀词典就可以得到词。

get_DAG(self, sentence)函数进行对系统初始化完毕后，会构建有向无环图。

从前往后依次遍历文本的每个位置，对于位置k，首先形成一个片段，这个片段只包含位置k的字，然后就判断该片段是否在前缀词典中，

\1. 如果这个片段在前缀词典中，

1.1 如果词频大于0，就将这个位置i追加到以k为key的一个列表中；

1.2 如果词频等于0，如同第2章中提到的“北京大”，则表明前缀词典存在这个前缀，但是统计词典并没有这个词，继续循环；

\2. 如果这个片段不在前缀词典中，则表明这个片段已经超出统计词典中该词的范围，则终止循环；

\3. 然后该位置加1，然后就形成一个新的片段，该片段在文本的索引为[k:i+1]，继续判断这个片段是否在前缀词典中。

jieba分词中get_DAG函数实现如下，

# 有向无环图构建主函数
    def get_DAG(self, sentence):
        # 检查系统是否已经初始化
        self.check_initialized()
        # DAG存储向无环图的数据，数据结构是dict
        DAG = {}
        N = len(sentence)
        # 依次遍历文本中的每个位置
        for k in xrange(N):
            tmplist = []
            i = k
            # 位置k形成的片段
            frag = sentence[k]
            # 判断片段是否在前缀词典中
            # 如果片段不在前缀词典中，则跳出本循环
            # 也即该片段已经超出统计词典中该词的长度
            while i < N and frag in self.wfreq:
                # 如果该片段的词频大于0
                # 将该片段加入到有向无环图中
                # 否则，继续循环
                if self.wfreq[frag]:
                    tmplist.append(i)
                # 片段末尾位置加1
                i += 1
                # 新的片段较旧的片段右边新增一个字
                frag = sentence[k:i + 1]
            if not tmplist:
                tmplist.append(k)
            DAG[k] = tmplist
        return DAG

以“去北京大学玩”为例，最终形成的有向无环图为，

{0: [0], 1: [1,2,4], 2: [2], 3: [3,4], 4: [4], 5: [5]}

最大概率路径计算

上面构建出的有向无环图DAG的每个节点，都是带权的，对于在前缀词典里面的词语，其权重就是它的词频；我们想要求得route = (w1,w2,w3,…,wn)，使得 最大。

如果需要使用动态规划求解，需要满足两个条件，

- 重复子问题

- 最优子结构

我们来分析一下最大概率路径问题，是否满足动态规划的两个条件。

重复子问题

对于节点wi和其可能存在的多个后继节点Wj和Wk，

任意通过Wi到达Wj的路径的权重 = 该路径通过Wi的路径权重 + Wj的权重，也即{Ri -> j} = {Ri + weight(j)}
任意通过Wi到达Wk的路径的权重 = 该路径通过Wi的路径权重 + Wk的权重，也即{Ri -> k} = {Ri + weight(k)}

即对于拥有公共前驱节点Wi的节点Wj和Wk，需要重复计算达到Wi的路径的概率。

最优子结构

对于整个句子的最优路径Rmax和一个末端节点Wx，对于其可能存在的多个前驱Wi，Wj，Wk…，设到达Wi，Wj，Wk的最大路径分别是Rmaxi，Rmaxj，Rmaxk，有，

Rmax = max(Rmaxi,Rmaxj,Rmaxk,...) + weight(Wx)

于是，问题转化为，求解Rmaxi，Rmaxj，Rmaxk，…等，

组成了最优子结构，子结构里面的最优解是全局的最优解的一部分。

状态转移方程为，

Rmax = max{(Rmaxi,Rmaxj,Rmaxk,...) + weight(Wx)}

jieba分词中计算最大概率路径的主函数是calc(self, sentence, DAG, route)，函数根据已经构建好的有向无环图计算最大概率路径。

函数是一个自底向上的动态规划问题，它从sentence的最后一个字（N-1）开始倒序遍历sentence的每个字（idx）的方式，计算子句sentence[idx ~ N-1]的概率对数得分。然后将概率对数得分最高的情况以（概率对数，词语最后一个位置）这样的元组保存在route中。

函数中，logtotal为构建前缀词频时所有的词频之和的对数值，这里的计算都是使用概率对数值，可以有效防止下溢问题。

jieba分词中calc函数实现如下，

def calc(self, sentence, DAG, route):
        N = len(sentence)
        # 初始化末尾为0
        route[N] = (0, 0)
        logtotal = log(self.total)
        # 从后到前计算
        for idx in xrange(N - 1, -1, -1):
            route[idx] = max((log(self.FREQ.get(sentence[idx:x + 1]) or 1) -
                              logtotal + route[x + 1][0], x) for x in DAG[idx])

上面的计算过程，logtotal约为17.91；首先是填充了route[6]，（0，0）；然后从最后一个字开始计算，‘去北京大学玩’，也即开始计算‘玩’；

ln(4207) - 17.91 = -9.56

DAG[5]中没有其他的x，所以更新route[5] = (-9.56，5)

接下来是’学’，DAG[4]同样只有4自己，所以计算

ln(17432) - 17.91 + （-9.56） = -17.70

更新route[4] = (-17.70，4)

对于’大‘，它有两种方式，分别是’大学’和’大’、’学’；这样的话，分别计算

ln(144099) - 17.91 + (-17.70) = -23.73
ln(20025) - 17.91 + (-9.56) = -17.57

更新ruote[3] = (-17.57, 4)

可以看一下运行效果。

{0: [0], 1: [1, 2, 4], 2: [2], 3: [3, 4], 4: [4], 5: [5]}

(4207, '玩')
(17482, '学')
(144099, '大')
(20025, '大学')
(6583, '京')
(17860, '北')
(34488, '北京')
(2053, '北京大学')
(123402, '去')
{6: (0, 0), 5: (-9.567048044164698, 5), 4: (-17.709674112779485, 4), 3: (-17.573864399983357, 4), 2: (-26.6931716802707, 2), 1: (-19.851543754900984, 4), 0: (-26.039894284878688, 0)}
去 北京大学 玩

最后就是从前向后找一个概率最大的情况。

本部分代码可以参考：

liuhuanyong/WordSegmentgithub.com

以及

xlturing/machine-learning-journeygithub.com

表示感谢。

---

基于汉字成词能力的HMM模型

以下内容来自参考9，在此表示感谢。

前面已经介绍了基于前缀词典和动态规划方法实现分词，我们之前看到过，如果没有前缀词典或者有些词不在前缀词典中，jieba分词一样可以分词，那么jieba分词是如何对未登录词进行分词呢？这就是本部分将要讲解的，基于汉字成词能力的HMM（Hidden Markov Model）模型识别未登录词。

可以对比一下对“哈利波特的移动城堡”的分词结果。

因为在原始的词典中有“哈利波”所以，n-gram算法分词为：

哈利波 特 的 移动 城堡

HMM的分词结果则为：

哈利波特 的 移动 城堡

但是当处理“哈利波特和赫敏是好朋友”时，HMM的分词结果是：

哈利波 特和赫敏 是 好 朋友

利用HMM模型进行分词，主要是将分词问题视为一个序列标注（sequence labeling）问题，其中，句子为观测序列，分词结果为状态序列。首先通过语料训练出HMM相关的模型，然后利用Viterbi算法进行求解，最终得到最优的状态序列，然后再根据状态序列，输出分词结果。

实例

序列标注，就是将输入句子和分词结果当作两个序列，句子为观测序列，分词结果为状态序列，当完成状态序列的标注，也就得到了分词结果。

以“去北京大学玩”为例，我们知道“去北京大学玩”的分词结果是“去 / 北京大学 / 玩”。对于分词状态，由于jieba分词中使用的是4-tag，因此我们以4-tag进行计算。4-tag，也就是每个字处在词语中的4种可能状态，B、M、E、S，分别表示Begin（这个字处于词的开始位置）、Middle（这个字处于词的中间位置）、End（这个字处于词的结束位置）、Single（这个字是单字成词）。具体如下图所示，“去”和“玩”都是单字成词，因此状态就是S，“北京大学”是多字组合成的词，因此“北”、“京”、“大”、“学”分别位于“北京大学”中的B、M、M、E。

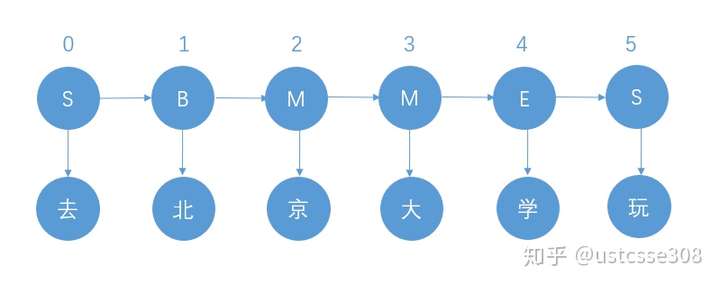
HMM模型有三个基本问题：

1.概率计算问题，给定模型 和观测序列 ，怎样计算在模型 下观测序列O出现的概率 ，也就是Forward-backward算法；

2.学习问题，已知观测序列 ，估计模型 ，使得在该模型下观测序列的概率 尽可能的大，即用极大似然估计的方法估计参数；

3.预测问题，也称为解码问题，已知模型 和观测序列 ，求对给定观测序列条件概率 最大的状态序列 ，即给定观测序列。求最有可能的对应的状态序列；

其中，jieba分词主要中主要涉及第三个问题，也即预测问题。

HMM模型中的五元组表示：

- 1.观测序列；

- 2.隐藏状态序列；

- 3.状态初始概率；

- 4.状态转移概率；

- 5.状态发射概率；

这里仍然以“去北京大学玩”为例，那么“去北京大学玩”就是观测序列。

而“去北京大学玩”对应的“SBMMES”则是隐藏状态序列，我们将会注意到B后面只能接（M或者E），不可能接（B或者S）；而M后面也只能接（M或者E），不可能接（B或者S）。

状态初始概率表示，每个词初始状态的概率；jieba分词训练出的状态初始概率模型如下所示。其中的概率值都是取对数之后的结果（可以让概率相乘转变为概率相加），其中-3.14e+100代表负无穷，对应的概率值就是0。这个概率表说明一个词中的第一个字属于{B、M、E、S}这四种状态的概率，如下可以看出，E和M的概率都是0，这也和实际相符合：开头的第一个字只可能是每个词的首字（B），或者单字成词（S）。这部分对应jieba/finaseg/prob_start.py，具体可以进入源码查看。差不多对应着ln(0.77)和ln(0.23)

P={'B': -0.26268660809250016,
     'E': -3.14e+100,
     'M': -3.14e+100,
     'S': -1.4652633398537678}

jieba中的状态转移概率，其实就是一个嵌套的词典，数值是概率值求对数后的值，如下所示，

P={'B': {'E': -0.510825623765990, 'M': -0.916290731874155},
     'E': {'B': -0.5897149736854513, 'S': -0.8085250474669937},
     'M': {'E': -0.33344856811948514, 'M': -1.2603623820268226},
     'S': {'B': -0.7211965654669841, 'S': -0.6658631448798212}}

P[‘B’][‘E’]代表的含义就是从状态B转移到状态E的概率，由P[‘B’][‘E’] = -0.5897149736854513，表示当前状态是B，下一个状态是E的概率对数是-0.5897149736854513，对应的概率值是0.6，相应的，当前状态是B，下一个状态是M的概率是0.4，说明当我们处于一个词的开头时，下一个字是结尾的概率要远高于下一个字是中间字的概率，符合我们的直觉，因为二个字的词比多个字的词更常见。

状态发射概率，根据HMM模型中观测独立性假设，发射概率，即观测值只取决于当前状态值，也就如下所示，

P(observed[i],states[j]) = P(states[j]) * P(observed[i] | states[j])

其中，P(observed[i] | states[j])就是从状态发射概率中获得的。

P={'B': {'一': -3.6544978750449433,
           '丁': -8.125041941842026,
           '七': -7.817392401429855,
    ...
    'S': {':': -15.828865681131282,
      '一': -4.92368982120877,
      '丁': -9.024528361347633,
    ...

P[‘B’][‘一’]代表的含义就是状态处于’B’，而观测的字是‘一’的概率对数值为P[‘B’][‘一’] = -3.6544978750449433

Viterbi算法

Viterbi算法实际上是用动态规划求解HMM模型预测问题，即用动态规划求概率路径最大（最优路径）。这时候，一条路径对应着一个状态序列。

根据动态规划原理，最优路径具有这样的特性：如果最优路径在时刻t通过结点 ，那么这一路径从结点 到终点 的部分路径，对于从 到 的所有可能的部分路径来说，必须是最优的。因为假如不是这样，那么从 到 就有另一条更好的部分路径存在，如果把它和从 到达 的部分路径连接起来，就会形成一条比原来的路径更优的路径，这是矛盾的。简而言之，最优路径的子路径也一定是最优的。

依据这个原理，我们只需要从时刻t=1开始，递推地计算在时刻t状态i的各条部分路径的最大概率，直至得到时刻t=T状态为i的各条路径的最大概率。时刻t=T的最大概率就是最优路径的概率 ，最优路径的终结点 也同时得到。之后，为了找出最优路径的各个结点，从终结点 开始，由后向前逐步求得结点 ，最终得到最优路径 。

输出分词结果

由Viterbi算法得到状态序列，也就可以根据状态序列得到分词结果。其中状态以B开头，离它最近的以E结尾的一个子状态序列或者单独为S的子状态序列，就是一个分词。以”去北京大学玩“的隐藏状态序列”SBMMES“为例，则分词为”S / BMME / S“，对应观测序列，也就是”去 / 北京大学 / 玩”。

源码

prob_start.py 存储了已经训练好的HMM模型的状态初始概率表；

prob_trans.py 存储了已经训练好的HMM模型的状态转移概率表；

prob_emit.py 存储了已经训练好的HMM模型的状态发射概率表；

HMM模型参数训练

HMM模型的参数是如何训练出来，此处可以参考jieba中Issue 模型的数据是如何生成的? ，如下是jieba的开发者的解释：

来源主要有两个，一个是网上能下载到的1998人民日报的切分语料还有一个msr的切分语料。另一个是我自己收集的一些txt小说，用ictclas把他们切分（可能有一定误差），然后用python脚本统计词频。
要统计的主要有三个概率表：1)位置转换概率，即B（开头）,M（中间),E(结尾),S(独立成词）四种状态的转移概率；2）位置到单字的发射概率，比如P(“和”|M)表示一个词的中间出现”和”这个字的概率；3) 词语以某种状态开头的概率，其实只有两种，要么是B，要么是S。

基于HMM模型的分词流程

jieba分词会首先调用函数cut(sentence)，cut函数会先将输入句子进行解码，然后调用_cut函数进行处理。cut函数就是jieba分词中实现HMM模型分词的主函数。cut函数会首先调用viterbi算法，求出输入句子的隐藏状态，然后基于隐藏状态进行分词。

def __cut(sentence):
        global emit_P
        # 通过viterbi算法求出隐藏状态序列
        prob, pos_list = viterbi(sentence, 'BMES', start_P, trans_P, emit_P)
        begin, nexti = 0, 0
        # print pos_list, sentence
        # 基于隐藏状态序列进行分词
        for i, char in enumerate(sentence):
            pos = pos_list[i]
            # 字所处的位置是开始位置
            if pos == 'B':
                begin = i
            # 字所处的位置是结束位置
            elif pos == 'E':
                # 这个子序列就是一个分词
                yield sentence[begin:i + 1]
                nexti = i + 1
            # 单独成字
            elif pos == 'S':
                yield char
                nexti = i + 1
        # 剩余的直接作为一个分词，返回
        if nexti < len(sentence):
            yield sentence[nexti:]

Viterbi算法

首先先定义两个变量， 定义在时刻t状态i的所有单个路径 中概率最大值为

由此可得变量 的递推公式为，

定义在时刻t状态i的所有单个路径 中概率最大的路径的第t-1个结点为，

Viterbi算法的大致流程：

输入：模型 和观测序列 ；

输出：最优路径 ；

（1）初始化

（2）递推

（3）终止

（4）最优路径回溯，对于t=T-1，T-2，…，1，

最终求得最优路径 ；

jieba分词实现Viterbi算法是在viterbi(obs, states, start_p, trans_p, emit_p)函数中实现。viterbi函数会先计算各个初始状态的对数概率值，然后递推计算，每时刻某状态的对数概率值取决于上一时刻的对数概率值、上一时刻的状态到这一时刻的状态的转移概率、这一时刻状态转移到当前的字的发射概率三部分组成。

def viterbi(obs, states, start_p, trans_p, emit_p):
        V = [{}]  # tabular
        path = {}
        # 时刻t = 0，初始状态
        for y in states:  # init
            V[0][y] = start_p[y] + emit_p[y].get(obs[0], MIN_FLOAT)
            path[y] = [y]
        # 时刻t = 1,...,len(obs) - 1
        for t in xrange(1, len(obs)):
            V.append({})
            newpath = {}
            # 当前时刻所处的各种可能的状态
            for y in states:
                # 获取发射概率对数
                em_p = emit_p[y].get(obs[t], MIN_FLOAT)
                # 分别获取上一时刻的状态的概率对数，该状态到本时刻的状态的转移概率对数，本时刻的状态的发射概率对数
                # 其中，PrevStatus[y]是当前时刻的状态所对应上一时刻可能的状态
                (prob, state) = max(
                    [(V[t - 1][y0] + trans_p[y0].get(y, MIN_FLOAT) + em_p, y0) for y0 in PrevStatus[y]])
                V[t][y] = prob
                # 将上一时刻最优的状态 + 这一时刻的状态
                newpath[y] = path[state] + [y]
            path = newpath

        # 最后一个时刻
        (prob, state) = max((V[len(obs) - 1][y], y) for y in 'ES')

        # 返回最大概率对数和最优路径
        return (prob, path[state])

相关优化：

- 1.将每一时刻最优概率路径记录下来，避免了第4步的最优路径回溯；

- 2.提前建立一个当前时刻的状态到上一时刻的状态的映射表，记录每个状态在前一时刻的可能状态，降低计算量；如下所示，当前时刻的状态是B，那么前一时刻的状态只可能是（E或者S），而不可能是（B或者M）；

PrevStatus = {
        'B': 'ES',
        'M': 'MB',
        'S': 'SE',
        'E': 'BM'
    }

以上介绍HMM的内容可能难以理解，所以我们另外找两个例子来理解。

如何用简单易懂的例子解释隐马尔可夫模型？www.zhihu.com

还是用最经典的例子，掷骰子。假设我手里有三个不同的骰子。第一个骰子是我们平常见的骰子（称这个骰子为D6），6个面，每个面（1，2，3，4，5，6）出现的概率是1/6。第二个骰子是个四面体（称这个骰子为D4），每个面（1，2，3，4）出现的概率是1/4。第三个骰子有八个面（称这个骰子为D8），每个面（1，2，3，4，5，6，7，8）出现的概率是1/8。

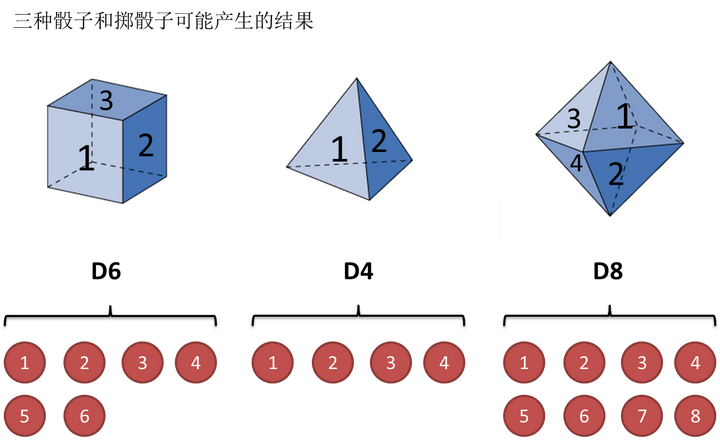
假设我们开始掷骰子，我们先从三个骰子里挑一个，挑到每一个骰子的概率都是1/3。然后我们掷骰子，得到一个数字，1，2，3，4，5，6，7，8中的一个。不停的重复上述过程，我们会得到一串数字，每个数字都是1，2，3，4，5，6，7，8中的一个。例如我们可能得到这么一串数字（掷骰子10次）：1 6 3 5 2 7 3 5 2 4
这串数字叫做可见状态链。但是在隐马尔可夫模型中，我们不仅仅有这么一串可见状态链，还有一串隐含状态链。在这个例子里，这串隐含状态链就是你用的骰子的序列。比如，隐含状态链有可能是：D6 D8 D8 D6 D4 D8 D6 D6 D4 D8
一般来说，HMM中说到的马尔可夫链其实是指隐含状态链，因为隐含状态（骰子）之间存在转换概率（transition probability）。在我们这个例子里，D6的下一个状态是D4，D6，D8的概率都是1/3。D4，D8的下一个状态是D4，D6，D8的转换概率也都一样是1/3。这样设定是为了最开始容易说清楚，但是我们其实是可以随意设定转换概率的。比如，我们可以这样定义，D6后面不能接D4，D6后面是D6的概率是0.9，是D8的概率是0.1。这样就是一个新的HMM。
同样的，尽管可见状态之间没有转换概率，但是隐含状态和可见状态之间有一个概率叫做输出概率（emission probability），也叫发射概率。就我们的例子来说，六面骰（D6）产生1的输出概率是1/6。产生2，3，4，5，6的概率也都是1/6。我们同样可以对输出概率进行其他定义。比如，我有一个被赌场动过手脚的六面骰子，掷出来是1的概率更大，是1/2，掷出来是2，3，4，5，6的概率是1/10。

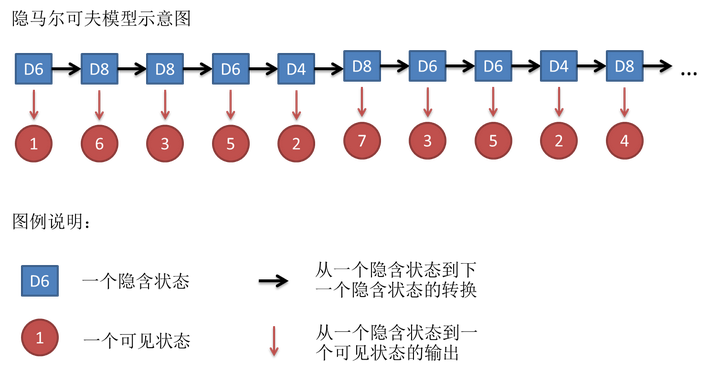
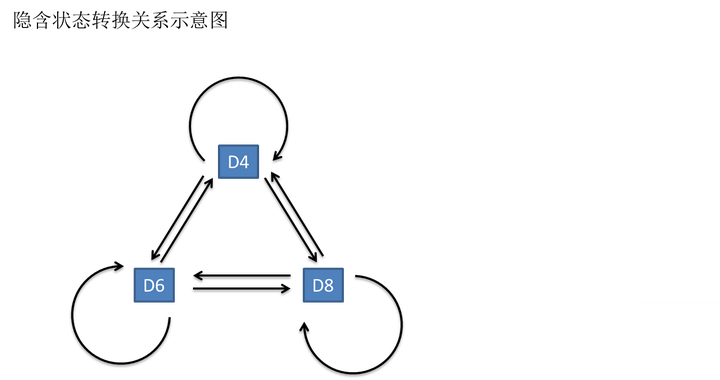
其实对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做模拟是相当容易的。但是应用HMM模型时候呢，往往是缺失了一部分信息的，有时候你知道骰子有几种，每种骰子是什么，但是不知道掷出来的骰子序列；有时候你只是看到了很多次掷骰子的结果，剩下的什么都不知道。如果应用算法去估计这些缺失的信息，就成了一个很重要的问题。

和HMM模型相关的算法主要分为三类，分别解决三种问题：
1）知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率和发射概率），根据掷骰子掷出的结果（可见状态链），我想知道每次掷出来的都是哪种骰子（隐含状态链）。
这个问题呢，在语音识别领域呢，叫做解码问题。一种解法求最大似然状态路径，说通俗点呢，就是求一串骰子序列，这串骰子序列产生观测结果的概率最大。
2）还是知道骰子有几种（隐含状态数量），每种骰子是什么（转换概率和发射概率），根据掷骰子掷出的结果（可见状态链），我想知道掷出这个结果的概率。
看似这个问题意义不大，因为掷出来的结果很多时候都对应了一个比较大的概率。问这个问题的目的呢，其实是检测观察到的结果和已知的模型是否吻合。如果很多次结果都对应了比较小的概率，那么就说明已知的模型很有可能是错的，有人偷偷把骰子給换了。
3）知道骰子有几种（隐含状态数量），不知道每种骰子是什么（转换概率和发射概率），观测到很多次掷骰子的结果（可见状态链），我想反推出每种骰子是什么（转换概率）。
这个问题很重要，因为这是最常见的情况。很多时候我们只有可见结果，不知道HMM模型里的参数，我们需要从可见结果估计出这些参数，这是建模的一个必要步骤。

0.一个简单问题
其实这个问题实用价值不高。由于对下面较难的问题有帮助，所以先在这里提一下。
知道骰子有几种，每种骰子是什么，每次掷的都是什么骰子，根据掷骰子掷出的结果，求产生这个结果的概率。

解法无非就是概率相乘：

1.看见不可见的，破解骰子序列

举例来说，我知道我有三个骰子，六面骰，四面骰，八面骰。我也知道我掷了十次的结果（1 6 3 5 2 7 3 5 2 4），我不知道每次用了那种骰子，我想知道最有可能的骰子序列。
其实最简单而暴力的方法就是穷举所有可能的骰子序列，然后依照第零个问题的解法把每个序列对应的概率算出来。然后我们从里面把对应最大概率的序列挑出来就行了 。如果马尔可夫链不长，当然可行。如果长的话，穷举的数量太大，就很难完成了。
另外一种很有名的算法叫做Viterbi algorithm. 要理解这个算法，我们先看几个简单的列子。
首先，如果我们只掷一次骰子：

看到结果为1。对应的最大概率骰子序列就是D4，因为D4产生1的概率是1/4，高于1/6和1/8.
把这个情况拓展，我们掷两次骰子：

结果为1，6。这时问题变得复杂起来，我们要计算三个值，分别是第二个骰子是D6，D4，D8的最大概率。显然，要取到最大概率，第一个骰子必须为D4。这时，第二个骰子取到D6的最大概率是


同样的，我们可以计算第二个骰子是D4或D8时的最大概率。我们发现，第二个骰子取到D6的概率最大。而使这个概率最大时，第一个骰子为D4。所以最大概率骰子序列就是D4 D6。
继续拓展，我们掷三次骰子：

同样，我们计算第三个骰子分别是D6，D4，D8的最大概率。我们再次发现，要取到最大概率，第二个骰子必须为D6。这时，第三个骰子取到D4的最大概率是

同上，我们可以计算第三个骰子是D6或D8时的最大概率。我们发现，第三个骰子取到D4的概率最大。而使这个概率最大时，第二个骰子为D6，第一个骰子为D4。所以最大概率骰子序列就是D4 D6 D4。
写到这里，大家应该看出点规律了。既然掷骰子一二三次可以算，掷多少次都可以以此类推。我们发现，我们要求最大概率骰子序列时要做这么几件事情。首先，不管序列多长，要从序列长度为1算起，算序列长度为1时取到每个骰子的最大概率。然后，逐渐增加长度，每增加一次长度，重新算一遍在这个长度下最后一个位置取到每个骰子的最大概率。因为上一个长度下的取到每个骰子的最大概率都算过了，重新计算的话其实不难。当我们算到最后一位时，就知道最后一位是哪个骰子的概率最大了。然后，我们要把对应这个最大概率的序列从后往前推出来。

上面的Viterbi算法的例子，优点是非常简单，第一次看的同学很容易获得关于HMM和Viterbi的基本概念；但是缺点是太过于简化了，可能有同学会把Viterbi理解的过于简单。

上面的例子过分简化的是三个隐含状态之间的转换概率都是相等的。导致从观测状态倒推出来的最大概率的隐含状态在之后的计算中会一直是最大概率，所以计算非常简单。如果不同隐含状态之间的转换概率不同，那么这个计算会更复杂。上面的例子，纯粹是帮助理解HMM、转换概率、发射概率等概念。

再举一个例子，来自于

如何通俗地讲解 viterbi 算法？www.zhihu.com

从前有个村子，村民们的身体情况只有两种可能：健康或者发烧。村民对自己的身体状况只会回答正常、头晕或冷；医生通过询问村民的感觉，判断村民的病情。
假设一个村民告诉医生感觉正常。
第二天告诉医生感觉有点冷。
第三天她告诉医生感觉有点头晕。
那么如何根据这个描述，判断村民的身体状况呢？

已知条件

隐含的身体状态 = { 健康 , 发烧 }

可观察的感觉状态 = { 正常 , 冷 , 头晕 }

村民身体状态的概率分布 = { 健康：0.6 , 发烧： 0.4 }

村民身体健康状态的转换概率分布 = {
健康->健康： 0.7 ,
健康->发烧： 0.3 ,
发烧->健康：0.4 ,
发烧->发烧： 0.6
}

在相应健康状况条件下，村民的感觉的概率分布 = {
健康，正常：0.5 ，冷 ：0.4 ，头晕： 0.1 ；
发烧，正常：0.1 ，冷 ：0.3 ，头晕： 0.6
}
村民连续三天的身体感觉依次是： 正常、冷、头晕 。

问题：

村民连续三天的健康状况如何？

计算过程：

• P(健康) = 0.6，P(发烧)=0.4。

\2. 求第一天的身体情况：
计算村民感觉正常的情况下最可能的身体状态。

• P(正常|初始健康) = P(正常|健康)P(健康|初始情况) = 0.5 * 0.6 = *0.3**
• P(正常|初始发烧) = P(正常|发烧)P(发烧|初始情况) = 0.1 * 0.4 = *0.04**

那么就可以认为第一天最可能的身体状态是：健康。

如果我们继续算下去，可以算出来P(第一天健康|正常)和P(第一天发烧|正常)的概率。

\3. 求第二天的身体状况：
计算在村民感觉冷的情况下最可能的身体状态。
那么第二天有四种情况，由于第一天的发烧或者健康转换到第二天的发烧或者健康。

• P(正常，冷|前一天发烧，今天发烧) = P(正常|前一天发烧)P(发烧->发烧)P(冷|发烧) = 0.04 * 0.6 * 0.3 = 0.0072
• P(正常，冷|前一天发烧，今天健康) = P(正常|前一天发烧)P(发烧->健康)P(冷|健康) = 0.04 * 0.4 * 0.4 = 0.0064
• P(正常，冷|前一天健康，今天健康) = P(正常|前一天健康)P(健康->健康)P(冷|健康) = 0.3 * 0.7 * 0.4 = 0.084
• P(正常，冷|前一天健康，今天发烧) = P(正常|前一天健康)P(健康->发烧)P(冷|发烧) = 0.3 * 0.3 .03 = *0.027**

那么可以认为，第二天最可能的状态是：健康。

4.求第三天的身体状态：
计算在村民感觉头晕的情况下最可能的身体状态。

• P(前一天发烧，今天发烧) = P(前一天发烧)P(发烧->发烧)P(头晕|发烧) = 0.027 * 0.6 * 0.6 = 0.00972
• P(前一天发烧，今天健康) = P(前一天发烧)P(发烧->健康)P(头晕|健康) = 0.027 * 0.4 * 0.1 = 0.00108
• P(前一天健康，今天健康) = P(前一天健康)P(健康->健康)P(头晕|健康) = 0.084 * 0.7 * 0.1 = 0.00588
• P(前一天健康，今天发烧) = P(前一天健康)P(健康->发烧)P(头晕|发烧) = 0.084 * 0.3 0.6 = *0.01512**

那么可以认为：第三天最可能的状态是发烧。

5.结论
根据如上计算，医生判断村民这三天身体变化的序列是：健康->健康->发烧。

维基百科的这个例子的动态图：

https://en.wikipedia.org/wiki/File:Viterbi_animated_demo.gifen.wikipedia.org

参考：

1. https://juejin.im/post/5d2f1ff16fb9a07ed740b375 【整体介绍】
2. https://www.cnblogs.com/pinard/p/6945257.html 【具体实例】
3. https://www.zhihu.com/question/20962240 【形象解释】
4. https://zhuanlan.zhihu.com/p/27056207 【复杂度分析】
5. https://www.cnblogs.com/xlturing/p/8465965.html
6. https://blog.csdn.net/shuihupo/article/details/81540433 【分词工具对比】
7. https://github.com/fxsjy/jieba 【Jieba github】
8. https://zhuanlan.zhihu.com/p/58848504 【结合实例讲解】
9. https://zhuanlan.zhihu.com/p/59475170
10. https://blog.csdn.net/chenwei825825/article/details/21383545
11. https://cloud.tencent.com/developer/article/1058352 【公式】
12. https://blog.csdn.net/songbinxu/article/details/80209197?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
13. https://blog.csdn.net/Zh823275484/article/details/87878512?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

编辑于 2020-03-10

自然语言处理

分词

中文分词